摘要
在大数据算法中,聚类算法一般都是作为其他算法分析的基础,对数据进行聚类可以从整体上分析数据的一些特性。聚类有很多的算法,k-means是最简单最实用的一种算法。在这里对k-means算法的原理以及其背后的数学推导做一
些详细的介绍,并讨论在实际应用中要避免的一些坑。
算法
k-means算法很简单,但是当我们正真把这个算法用在生产中时还是存在很多的细节需要考虑的,这些细节将要在后面进行讨论。首先给出k-means算法的步骤:
1、给出k个初始聚类中心
2、repeat:
把每一个数据对象重新分配到k个聚类中心处,形成k个簇
重新计算每一个簇的聚类中心
3、until 聚类中心不在发生变化
k和初始聚类中心的选择的讨论
1、k的选择
当我们拿到一批数据时,大多数情况下我们是不知道簇的个数的。
a、在一些情况下,我们通过对业务了解的加深,是可以找到数据的簇的,比如我们手里有一批用户购买商品的记录数据,已经统计出用户工作日和周末购买物品的数量,在二维做坐标中分别为:工作日购买的物品数和周末购买的物品数,从这我们可以发现,我们人为已经把数据分为三个簇:周末购买、工作日购买和周末和工作日都购买的人数
b、当我们真的确定不了数据的簇时,我们可以通过相关的算法来大概确定数据的簇。对k进行多次取值,通过一个目标函数f进行度量,选取使这个f值最小的k作为聚类中心(目标函数f后面会讲到),进行多次选择k值时,时间和空间复杂度都会增加。还一种策略是通过一个算法canopy算法初始选取出聚类的个数k和初始的聚中心作为k-means算法的输入,而canopy算法不需要输入k和初始聚类中心,它可以作为k-means算法预处理算法用来选取k-means算法。所需要的k值和聚类中心
2、聚类中心的选择
选取初始聚类中心是最让人头疼的一件事,如果选择的不好就容易找到局部最优聚类中心而不是全局最优的聚类中心。
a、知道了k后,再选取初始的聚类中心。一种策略是进行多次随机的选择k个点作为初始聚类中心,比较目标函数f,选取目标函数f最小的最为初始的聚类中心,这种随机选择有很多的不足:1、无形中就增加了时间开销和空间开销 2、找到的聚类中心可能是局部最优的而不是全局最优的,因为当随机选择的两个聚类中心位于一个簇中,无论怎么重新计算聚类中心,得到的结果都不是全局最优的,分类的结果也不是我们想要的。虽然这种策略有很多的不足,不代表我们不可以使用,在实际应用中我们还是可以选择这中策略进行生产的。
b、当知道了k后,还有一种选取聚类中心的策略:首先我们把数据分为两个部分:聚类中心集合和原始数据集合,首先我们从原始数据集合中随机的选择一个数据最为初始聚类中心的一个簇中心放入聚类中心集合中,然后我们再从原始数据集中选择一个聚类聚类中心集合中所有的记录都最远的一个点作为下一个初始的聚类中心。这种选择在实际应用中证明了也是比较好的一种策略,得到的效果要比a策略得到的好一些,但是这种策略要受到离群点的扰动比较的大,同时选择初始聚类中心的计算量也是非常大的,空间消耗也非常的大。
c、当k不知道的情况下,最常用的一种策略就是使用canopy算法来寻找k和聚类中心。
k-means最近邻的度量
在k-means算法中,我们需要把数据集分到距离聚类中心最近的那个簇中,这样就需要最近邻的度量策略。我们需要用什么来衡量最近,怎么衡量?k-means算法需要计算距离,计算距离就需要数值,因此k-means算法也是对数值型数据比较实用。k-means算法中最常用的度量公式:在欧式空间中采用的是欧式距离,在处理文档中采用的是余弦相似度函数,有时候也采用曼哈顿距离作为度量,不同的情况实用的度量公式是不一样的。
欧式距离
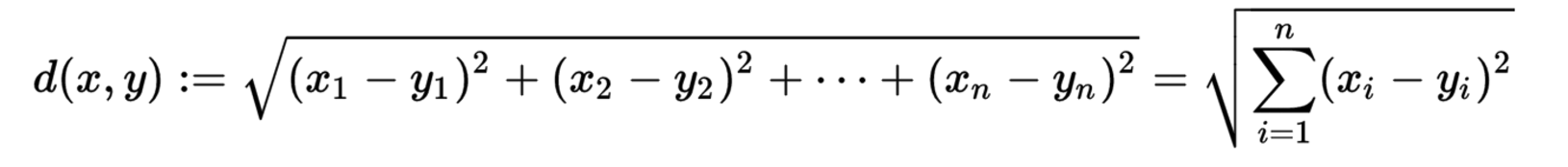
余弦相似度计算公式
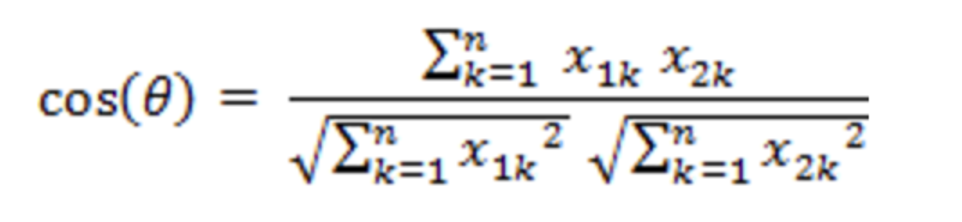
向量表示法
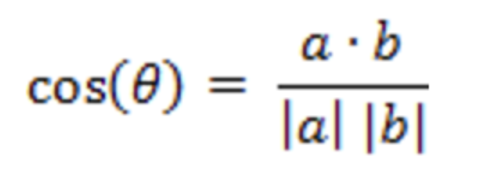
曼哈顿距离:
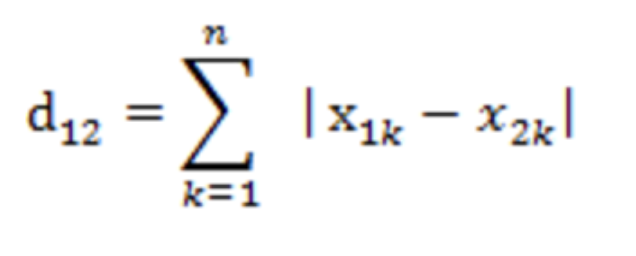
k-means算法背后的数据知识(k-means算法好坏的评价标准)
k-means算法要解决的问题是我们把数据给分成不同的簇,那我们要达到的目标是什么呢?是使得同一个簇的差异很小,不同簇之间的数据差异最大化,这是文字描述的,不能用来标准化研究或者数学推导,我们想要刚才的一句话用一个数据公式或者数学模型来进行衡量,建立怎么样的数学公式才能用来衡量上面的描述?一般情况下采用的是误差平方和作为衡量的目标函数SSE,上面提到的目标函数f就是SSE也是误差平方和。先上公式:
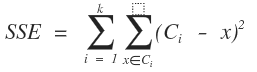
元素解释:C表示的聚类中心的值,x是属于这个簇的数据点,d为欧式距离
为了实现同一个簇的差异很小,不同簇之间的元素数据差异最大化(我们默认的数据都是在欧式空间中,数据的差异采用的是欧式距离来进行衡量)。为了实现这个目标,实际上是使误差平方和SSE最小,在了k-means算法中,有两个地方降低了SSE数值:把数据点分到距离中心点最近的簇中,这样计算出来的SSE将减少、重新计算聚类中心点,又进一步的降低了SSE,但是这样的优化策略只是为了找到局部最优解,如果想要找到全局最优解需要找到合理的初始聚类中心。
还有一个问题需要我们来讨论,我们为什么选取簇集合的平均值作为聚类中心呢,因为这样才能是SSE达到最小,在数学中求一个函数的最小值,怎么办?是不是求导,我们发现SSE是一个二元函数,那就求偏导吧,如下推导。
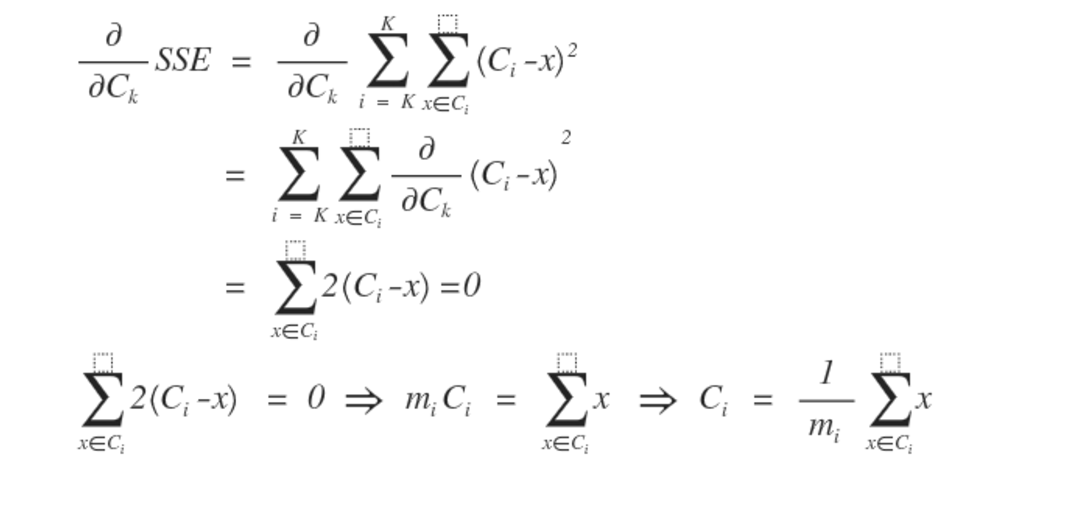
从上面的推导,可以看出我们为什么选择均值作为聚类中心,当聚类中心为簇中的均值时,才能是SSE最小,在接下来会对sparkMLlib中对于k-means的算法进行详细的介绍,再补吧